Минимум функции - это значение, при котором функция принимает наименьшее возможное значение. Поиск минимума функции - одна из важных задач оптимизации и математического анализа. Найти минимум функции можно различными методами, в зависимости от свойств функции и доступных алгоритмов.
Самый простой способ найти минимум функции - это использовать аналитическое решение, если оно существует. Аналитическое решение позволяет найти точное значение минимума функции без использования итерационных методов. Однако, аналитическое решение не всегда возможно или практично.
В случаях, когда аналитическое решение не доступно, можно использовать численные методы для поиска минимума функции. Эти методы применяются для аппроксимации значения минимума через последовательное приближение. Некоторые из наиболее распространенных численных методов для поиска минимума функции включают в себя метод Ньютона, метод золотого сечения и метод градиентного спуска.
Конечный выбор метода поиска минимума функции зависит от нескольких факторов, таких как свойства самой функции, степень точности, доступные ресурсы и требования к скорости выполнения. Независимо от выбранного метода, поиск минимума функции является важной задачей, имеющей множество применений в областях, таких как оптимизация, инженерия, экономика и машинное обучение.
Понятие минимума функции

Абсолютный минимум функции - это самое маленькое значение, которое функция может принимать на всем своем домене. Он является глобальным минимумом и может использоваться для определения наилучшего решения или состояния в задачах оптимизации.
Относительный минимум функции - это наименьшее значение, которое функция принимает внутри определенной области или интервала. Относительный минимум может быть локальным и относиться только к некоторой части графика функции. Он может быть полезен для определения локальных экстремумов или переходных состояний в системах.
Для нахождения минимума функции можно использовать различные методы, в зависимости от характера функции и требуемой точности результата. Некоторые из наиболее распространенных методов включают метод дихотомии, метод золотого сечения, метод Ньютона и метод градиентного спуска.
| Термин | Описание |
|---|---|
| Абсолютный минимум | Наименьшее значение функции на всем домене |
| Относительный минимум | Наименьшее значение функции внутри определенной области или интервала |
| Локальный минимум | Относительный минимум, относящийся только к некоторой части графика функции |
| Методы нахождения минимума функции | Метод дихотомии, метод золотого сечения, метод Ньютона, метод градиентного спуска |
Зачем находить минимум функции?
Найдя минимум функции, мы можем решить следующие задачи:
| 1. | Оптимизация: Поиск минимума функции может помочь найти оптимальное значение для конкретного критерия или задачи. Например, при проектировании автомобильных деталей мы можем искать минимум функции, представленной как стоимость производства деталей, чтобы найти оптимальное решение с минимальными затратами. |
| 2. | Моделирование: Нахождение минимума функции является неотъемлемой частью математического моделирования и анализа данных. Например, в задаче линейной регрессии мы можем искать минимум функции, представляющей сумму квадратов разностей между реальными и предсказанными значениями. |
| 3. | Нахождение экстремумов: Минимум функции является одним из типов экстремумов, вместе с максимумом и седловыми точками. Поиск минимума функции позволяет найти наименьшие значения и определить наиболее значимые точки в задачах оптимизации. |
Вычисление минимума функции может осуществляться различными методами, такими как методы дихотомии, метод Ньютона или метод градиентного спуска, в зависимости от типа функции и требуемой точности результата.
Таким образом, нахождение минимума функции является важной задачей, позволяющей решить задачи оптимизации, моделирования и нахождения экстремумов в различных областях науки и техники.
Методы нахождения минимума функции
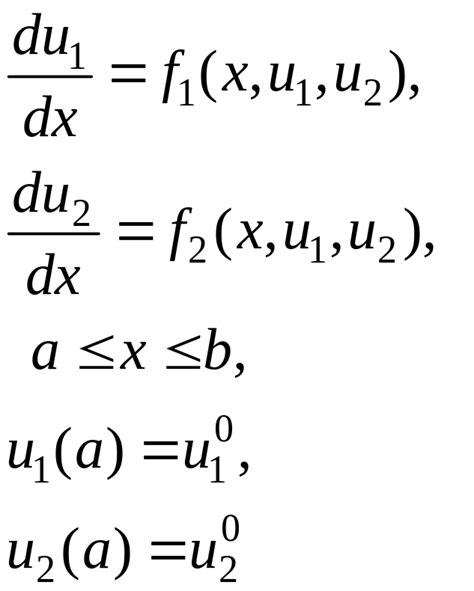
Существует несколько методов, позволяющих найти минимум функции. Вот некоторые из них:
Метод поиска экстремума
Этот метод основан на идее, что минимум и максимум функции соответствуют экстремумам этой функции. Для нахождения экстремумов используются производные функции, анализ их знаков и значений в точках. Этот метод удобен, когда функция имеет аналитическое представление и может быть проанализирована.
Метод дихотомии (метод половинного деления)
Этот метод основан на принципе деления интервала на две равные части и поиске минимума в каждой из них. Интервал затем сужается, пока не будет достигнута требуемая точность. Метод дихотомии прост в реализации и применим для широкого класса функций, но может требовать большого числа итераций для достижения требуемой точности.
Метод градиентного спуска
Градиентный спуск – это итерационный метод оптимизации, основанный на направлении наискорейшего убывания функции. Он начинает с некоторой точки и движется в направлении, противоположном градиенту функции, с целью поиска минимума. Метод градиентного спуска хорошо работает для выпуклых функций, но может застрять в локальных минимумах.
Метод имитации отжига
Метод имитации отжига основан на аналогии с процессом отжига в металлургии. Он моделирует случайные флуктуации значения функции и использует вероятностный подход для поиска минимума. Итерации продолжаются до достижения требуемой точности или до истечения времени. Метод имитации отжига позволяет избежать застревания в локальных минимумах, но требует достаточно большого количества итераций.
Это лишь некоторые из методов нахождения минимума функции. Выбор метода зависит от конкретной задачи, требуемой точности и доступных вычислительных ресурсов.
Метод дихотомии
Для применения метода дихотомии необходимо знать границы отрезка, на котором находится минимум функции. Затем отрезок делится пополам, и значение функции вычисляется в двух точках: середине отрезка и точке, лежащей справа или слева от середины. Затем выбирается новый отрезок, в котором минимум функции находится, и процесс повторяется до достижения заданной точности или определенного количества итераций.
Метод дихотомии является итерационным методом, поэтому его точность зависит от выбранного критерия остановки и числа итераций. Важным преимуществом этого метода является его робастность - он может применяться для нахождения минимума функции, даже если она не гладкая или имеет разрывы.
Однако метод дихотомии имеет и некоторые ограничения. Во-первых, он требует задания начального отрезка, на котором находится минимум. Во-вторых, этот метод может требовать большого числа итераций для достижения заданной точности, особенно если функция имеет выпуклости или узкий пик.
В целом, метод дихотомии является простым и эффективным методом нахождения минимума функции, особенно в случае, когда необходимо найти минимум на отрезке.
Метод золотого сечения

Для применения метода золотого сечения необходимо задать начальный интервал, в котором предполагается находится минимум функции. Далее, по формуле золотого сечения, определяется две точки, которые делят интервал в определенном соотношении. Затем, вычисляются значения функции в этих точках и на основе результатов делается выбор, в какой половине интервала находится искомый минимум. Данный процесс повторяется до тех пор, пока не будет достигнута заданная точность.
Преимуществом метода золотого сечения является его простота и независимость от производных функции. Однако, данный метод имеет некоторые недостатки. Во-первых, он требует больше итераций, чем некоторые другие методы. Во-вторых, он не гарантирует нахождение глобального минимума, а только локального. Поэтому, его применение может быть ограничено.
В целом, метод золотого сечения является эффективным методом для решения задачи нахождения минимума функции. Он широко применяется в различных областях, таких как оптимизация и численное моделирование.
Метод Ньютона
Методом Ньютона, также известным как метод касательных или метод Ньютона-Рафсона, можно найти локальный минимум функции. Он основывается на идее приближения функции с помощью её касательной линии в точке итерации.
Пусть функция f(x) непрерывна и дифференцируема на интервале [a, b]. Ищем минимум функции f(x) методом Ньютона.
Алгоритм метода Ньютона:
Задаём начальное значение x0 в интервале [a, b].
Находим значение производной f'(x) в точке x0.
Находим уравнение касательной линии к графику функции в точке x0.
Решаем уравнение касательной линии для нахождения следующего значения x1.
Повторяем шаги 2-4 до достижения заданной точности.
Метод Ньютона сходится быстрее, чем многие другие методы оптимизации. Однако, он требует вычисления производной функции и может застревать в локальных минимумах, если начальное значение выбрано неправильно.
Метод градиентного спуска
Основная идея метода градиентного спуска заключается в том, что если мы знаем частные производные функции в каждой точке, то можем определить в каком направлении находится минимум функции. Для этого используется градиент функции – вектор, каждая компонента которого равна частной производной функции по соответствующему параметру.
Алгоритм метода градиентного спуска состоит из последовательных шагов:
- Инициализация начального значения параметров.
- Вычисление градиента функции в текущей точке.
- Изменение значения параметров в направлении, противоположном градиенту.
- Повторение шагов 2 и 3 до достижения условия остановки.
Одним из условий остановки может быть достижение предела на количество итераций или достижение достаточно малого значения градиента. В каждой итерации градиента спуска значение функции убывает, приближаясь к минимуму. Однако, метод градиентного спуска может не всегда гарантировать нахождение глобального минимума, а только локального.
Метод градиентного спуска является одним из базовых подходов в оптимизации и используется во множестве областей, включая машинное обучение и нейронные сети.
Как выбрать метод?
Выбор метода минимизации функции зависит от различных факторов, таких как вид функции, требования к точности результата, доступные ресурсы и время выполнения. Используемый метод должен соответствовать особенностям задачи и обеспечивать наилучший результат.
Важным аспектом выбора метода является то, обладает ли функция, которую необходимо минимизировать, определенными свойствами. Например, если функция является выпуклой или дифференцируемой, можно использовать специализированные методы, такие как градиентный спуск или метод Ньютона.
Если же функция не обладает специальными свойствами, можно прибегнуть к методам, которые не требуют вычисления производных. К ним относятся методы покоординатного спуска, метод Нелдера-Мида и метод имитации отжига.
Однако следует учитывать, что использование методов без вычисления производных может привести к более длительному времени выполнения и менее точным результатам. Поэтому в таких случаях может быть полезно рассмотреть комбинацию методов для достижения оптимального решения.








