Корень функции — это значение переменной, при котором функция равна нулю. Нахождение корней функций является одной из основных задач математического анализа и нахождения решений уравнений. Корни функции могут иметь разное количество, в зависимости от ее типа и структуры.
Определение корней функции имеет важное применение не только в математике, но и в различных областях науки и техники. В физике, химии и экономике нахождение корней функций позволяет определить значения переменных и параметров, которые удовлетворяют заданным условиям и уравнениям. В программировании и компьютерной графике, знание корней функций позволяет решать сложные задачи визуализации и моделирования.
Найти корни функции можно разными способами. Один из наиболее распространенных методов — это метод итераций. Он заключается в последовательном приближении значения корня, начиная с какого-то начального значения. Другой метод — это метод половинного деления, который использует свойство функции менять знак на интервале, где есть корень.
Что такое корень функции?
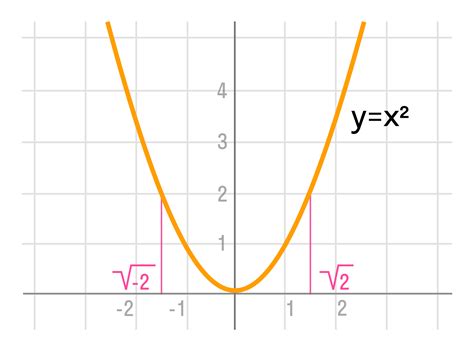
Корнем функции называется значение переменной, при котором функция равна нулю. Иными словами, это точка на графике функции, где она пересекает ось абсцисс.
Нахождение корня функции является важной задачей в математике и численных методах. В некоторых случаях корни можно найти аналитически путем решения уравнения, а в других случаях приходится использовать численные методы, такие как метод половинного деления, метод Ньютона и метод простой итерации. Эти методы позволяют найти приближенное значение корня функции с заданной точностью.
Корни функции имеют большое значение в физике, экономике, компьютерных науках и других областях. Они позволяют найти значения переменных, при которых уравнения и системы уравнений имеют определенные свойства или удовлетворяют определенным условиям. Например, корни квадратного уравнения позволяют найти значения переменных в равенстве или неравенстве.
| Пример | Объяснение |
|---|---|
| Функция: f(x) = x^2 - 4 | Корни функции: x = -2, x = 2 |
| Функция: g(x) = sin(x) | Корень функции: x = 0 |
Важность нахождения корня функции
Знание корней функции часто применяется во многих областях, включая физику, экономику, инженерное дело и компьютерные науки. Например, в физике, корни функции могут использоваться для определения момента, когда объект достигнет определенного положения или скорости. В экономике, корни функции могут применяться для определения равновесной цены или показателей прибыльности.
Нахождение корня функции также играет важную роль в алгоритмах оптимизации и численных методах. Методы, основанные на поиске корней функции, могут использоваться для нахождения оптимальных значений переменных в задачах оптимизации. Это особенно полезно в области машинного обучения и искусственного интеллекта.
В общем случае, нахождение корней функций является важным инструментом в математике и применяется во многих областях. Понимание того, как найти корень функции, может помочь в решении сложных задач и оптимизации процессов.
Как найти корень функции методом деления пополам?
Для применения этого метода необходимо, чтобы функция была непрерывной на заданном интервале. Алгоритм метода деления пополам заключается в следующем:
- Выбирается начальный интервал, в котором предположительно находится корень функции.
- Вычисляются значения функции на концах интервала.
- Интервал делится пополам и вычисляется значение функции в середине интервала.
- Выбирается новый интервал, в котором находится корень функции, на основании анализа знаков функции в концах и середине интервала.
- Шаги 2-4 повторяются до тех пор, пока разность между концами интервала не станет достаточно малой.
Метод деления пополам гарантирует нахождение корня функции, если она обладает следующими свойствами: непрерывность на заданном интервале и наличие только одного решения. Однако, этот метод может быть медленным при поиске корней функций с большим количеством поворотов в заданном интервале.
Метод Ньютона-Рафсона для нахождения корня функции
Алгоритм метода Ньютона-Рафсона выглядит следующим образом:
- Выбирается начальное приближение для корня функции.
- Пока не достигнута необходимая точность, выполняются шаги 3-5.
- Вычисляется значение функции и ее производной в текущей точке.
- Вычисляется следующая точка, используя формулу
xn+1 = xn - f(xn) / f'(xn), гдеxn- текущая точка,f(xn)- значение функции в текущей точке,f'(xn)- значение производной в текущей точке. - Если достигнута необходимая точность, алгоритм завершается и текущая точка считается корнем функции. В противном случае, переходим к шагу 3.
Метод Ньютона-Рафсона сходится быстро и точно для функций, которые хорошо приближаются линейной функцией вблизи корня. Однако, этот метод не всегда сходится и может быть неустойчив, если начальное приближение выбрано неправильно.
Тем не менее, метод Ньютона-Рафсона широко применяется в различных областях, таких как математика, физика, экономика и многих других, для нахождения корня функции. Он позволяет решать множество задач, где требуется численное решение уравнений или оптимизация функций.
Метод секущих в поиске корня функции
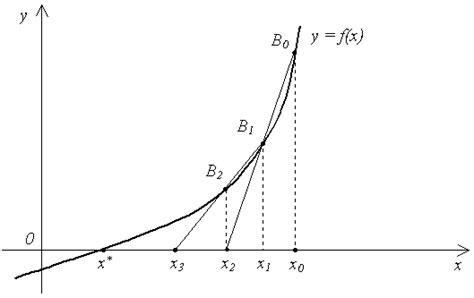
Для использования метода секущих необходимо задать начальное приближение корня и выбрать две точки на графике функции, которые будут использоваться для построения секущей. Затем производится последовательное вычисление значений функции в выбранных точках и получение новых точек пересечения с осью абсцисс.
В общем виде, итерационный процесс метода секущих можно описать следующим образом:
- Выбрать начальное приближение корня x₀ и x₁.
- Вычислить значения функции f(x₀) и f(x₁).
- Вычислить новую точку пересечения секущей:
- Повторять шаги 2-3 до достижения требуемой точности.
x₂ = x₁ - (x₁ - x₀) * f(x₁) / (f(x₁) - f(x₀))
Метод секущих является итерационным методом, который сходится к корню функции, если начальное приближение достаточно близко к истинному значению корня и функция удовлетворяет определенным условиям, таким как непрерывность и монотонность.
Одним из преимуществ метода секущих является его простота реализации и высокая скорость сходимости. Однако он может быть неустойчив в случае, если выбраны неправильные начальные приближения или функция имеет особенности, такие как разрывы или вертикальные асимптоты.
Квадратичная интерполяция для нахождения корня функции
Для использования квадратичной интерполяции необходимо знать значение функции в трех точках, расположенных слева и справа от корня функции. Зная эти значения, можно построить параболу, проходящую через эти точки, и найти ее корни с помощью решения квадратного уравнения.
Квадратичная интерполяция имеет преимущество над другими методами, такими как метод бисекции и метод Ньютона, в том, что она требует меньше итераций для нахождения корня функции. Однако она требует больше вычислительных ресурсов для построения параболы и решения квадратного уравнения.
Процесс квадратичной интерполяции состоит из следующих шагов:
- Выбрать три известные точки на графике функции, которые находятся слева и справа от корня функции.
- Построить параболу, проходящую через эти точки.
- Найти корни параболы, решив квадратное уравнение.
- Проверить, лежит ли корень функции между краевыми точками. Если нет, выбрать новые точки и повторить процесс.
- Повторять шаги, пока не будет достигнута необходимая точность.
Квадратичная интерполяция - это эффективный метод для нахождения корня функции, особенно в случаях, когда другие методы могут быть неэффективны или неустойчивы.
Метод итерации для поиска корня функции

Основной итерационной формулой метода является:
xn+1 = g(xn)
где xn - это текущее приближение для корня функции, xn+1 - следующее приближение, а g(x) - функция приближения, которая определяется из исходной функции.
Очевидно, что данный процесс требует начального значения корня функции. Важно выбрать подходящее начальное значение, чтобы метод сошёлся к искомому значению. Если начальное значение выбрано неправильно, метод может не сойтись или сойтись к неправильному корню.
Этот метод особенно полезен для поиска корней функций, для которых невозможно найти аналитическое решение или которые слишком сложны для аналитического решения. Он также может быть использован для нахождения корней функций, когда значение функции не может быть вычислено аналитически, но может быть вычислено численно.
Основной шаг метода итерации состоит из последовательного применения итерационной формулы до достижения требуемой точности или максимального числа итераций. Условие остановки выбирается в зависимости от конкретной задачи и требуемой точности результата.
Преимуществами метода итерации являются его относительная простота и универсальность, но при этом есть и некоторые ограничения. Он может сойтись медленно, особенно если начальное значение выбрано неправильно. Кроме того, метод может сходиться к локальному минимуму или максимуму функции, а не к искомому корню. Поэтому необходимо быть внимательным при выборе функции приближения.








