Дифференцируемость – это одно из важных понятий в математическом анализе, которое позволяет определить скорость изменения значения функции в заданной точке. Когда функция дифференцируема, мы можем найти ее производную, которая показывает, насколько быстро функция меняется по отношению к изменению ее аргумента. Производная позволяет нам изучать различные свойства функций, оптимизировать процессы и решать задачи из различных областей науки и техники.
Для того чтобы функция была дифференцируема в заданной точке, она должна быть определена в этой точке и иметь конечные пределы справа и слева от нее. Также для дифференцируемости функции необходимо, чтобы такие пределы были равны между собой. Если выполнены эти условия, мы говорим, что функция дифференцируема в этой точке и можем произвести ее дифференцирование.
Примером функции, которая дифференцируема в каждой точке своей области определения, является функция синуса. Ее производная равна косинусу, и она позволяет изучать такие явления как колебания и волны. Другим примером является функция x^2, которая является монотонно возрастающей на всей числовой оси и имеет производную 2x. Эта функция широко применяется в физике, экономике и других науках.
Что значит функция дифференцируется:

Когда говорят, что функция дифференцируется, это означает, что она обладает производной в каждой точке своей области определения. Производная функции в данной точке определяется как скорость изменения значения функции при изменении аргумента. Математически производная функции f(x) в точке x₀ определяется как:
f'(x₀) = lim (h → 0) [f(x₀ + h) - f(x₀)] / h
Числовым значением производной в точке x₀ является тангенс угла наклона касательной к графику функции в данной точке.
Примеры функций, дифференцируемых в своей области определения:
- Линейная функция: f(x) = kx + b, где k и b - константы. Производная линейной функции равна её коэффициенту при аргументе x, т.е. f'(x) = k.
- Квадратичная функция: f(x) = ax² + bx + c, где a, b, c - константы. Производная квадратичной функции равна сумме производных её слагаемых, т.е. f'(x) = 2ax + b.
- Экспоненциальная функция: f(x) = aᵡ, где a - положительная константа. Производная экспоненциальной функции равна произведению функции на её логарифмическую основу, т.е. f'(x) = aᵡ * ln(a).
Дифференцируемость функции позволяет исследовать её свойства и применять в различных областях науки и техники, включая физику, экономику, программирование и инженерию.
Определение и примеры функций
Примерами функций, которые являются дифференцируемыми, являются:
- Линейная функция: f(x) = mx + c, где m и c – константы.
- Полиномиальная функция: f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0, где a_i – коэффициенты и n – степень.
- Синусоидальная функция: f(x) = Asin(Bx + C), где A, B и C – константы.
Это лишь несколько примеров дифференцируемых функций. Дифференцируемость функции играет важную роль в математике и физике, позволяя изучать изменение функции в точке и определять ее скорость изменения.
Как найти производную функции?
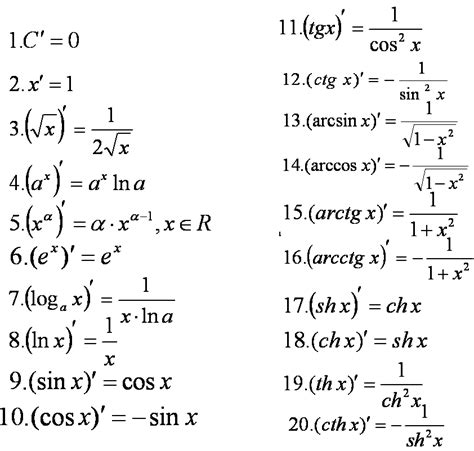
Для нахождения производной функции нужно выполнить некоторые математические операции, используя определение производной. Производная функции показывает, как быстро меняется значение функции с изменением ее аргумента.
Существуют различные методы вычисления производной в зависимости от типа функции. Некоторые из них:
- Формулы дифференцирования. Некоторые функции имеют известные формулы для вычисления их производных. Например, производная степенной функции или экспоненциальной функции может быть вычислена с использованием соответствующих формул.
- Правила дифференцирования. Существуют правила, которые позволяют вычислять производные сложных функций на основе производных простых функций. Такие правила включают правило суммы, правило произведения, правило деления и т. д.
- Дифференцирование неявных функций. Некоторые функции заданы неявно в виде уравнений. Для нахождения производной таких функций можно использовать метод неявного дифференцирования.
- Дифференцирование численно. В некоторых случаях, когда нет известной формулы или правила для вычисления производной, можно приближенно вычислить ее численно, используя методы численного дифференцирования.
При нахождении производной функции важно учитывать особые точки, такие как точки разрыва и точки, в которых производная не существует. Также может потребоваться применение дополнительных теоретических знаний для вычисления производной сложных функций.
Правила дифференцирования
Вот некоторые основные правила дифференцирования:
- Правило степенной функции: Если функция представлена в форме f(x) = x^n, где n является постоянной, то ее производная равна f'(x) = nx^(n-1).
- Правило константы: При дифференцировании постоянной функции f(x) = c, где c - это константа, ее производная равна нулю, то есть f'(x) = 0.
- Правило суммы: Если функция представлена в форме f(x) = g(x) + h(x), то ее производная равна сумме производных этих функций, то есть f'(x) = g'(x) + h'(x).
- Правило разности: Если функция представлена в форме f(x) = g(x) - h(x), то ее производная равна разности производных этих функций, то есть f'(x) = g'(x) - h'(x).
- Правило произведения: Если функция представлена в форме f(x) = g(x) * h(x), то ее производная вычисляется по формуле f'(x) = g'(x) * h(x) + g(x) * h'(x).
- Правило частного: Если функция представлена в форме f(x) = g(x) / h(x), то ее производная вычисляется по формуле f'(x) = (g'(x) * h(x) - g(x) * h'(x)) / (h(x))^2.
- Правило композиции: Если функция представлена в форме f(x) = g(h(x)), то ее производная вычисляется по формуле f'(x) = g'(h(x)) * h'(x), где g'(x) и h'(x) - производные соответствующих функций.
Используя эти правила, можно дифференцировать сложные функции и получать более удобные выражения для их производных. Эти правила являются основой для дальнейшего изучения дифференцирования и могут применяться для нахождения производной любой дифференцируемой функции.
Линейная и нелинейная дифференцируемость

Функция считается дифференцируемой в точке, если ее производная существует в этой точке. Однако, этот процесс может быть либо линейным, либо нелинейным.
Линейная дифференцируемость означает, что производная функции в точке может быть представлена линейной функцией относительно приращения аргумента.
Например, функция y = 2x+3 является линейно дифференцируемой, потому что любая ее производная будет представлена линейной функцией.
Нелинейная дифференцируемость означает, что производная функции в точке не может быть представлена линейной функцией относительно приращения аргумента.
Например, функция y = x^2 является нелинейно дифференцируемой, потому что производная функции в точке представлена нелинейной функцией.








