Аналитически заданная функция - это функция, которая может быть выражена с помощью аналитических выражений, таких как алгебраические операции, функции, подынтегральные величины и элементарные функции.
Аналитическое выражение это выражение, состоящее из констант, переменных (независимых или зависимых), математических операций и функций, определенных на множестве чисел.
Значение аналитически заданной функции может быть определено путем подстановки значений аргументов функции в аналитическое выражение. Например, для функции f(x) = 2x + 3 значение в точке x = 2 определяется следующим образом: f(2) = 2 * 2 + 3 = 7.
Другими словами, значение аналитически заданной функции - это результат вычисления данной функции для определенных значений аргументов.
Аналитически заданные функции широко используются в математике, физике и других науках для моделирования и решения различных задач.
Определение аналитически заданной функции

Аналитические функции широко используются в математике, физике, технике и других науках для моделирования различных явлений и решения разнообразных задач. Они позволяют получить точные значения функции в любой точке ее области определения.
Примеры аналитически заданных функций:
| Функция | Аналитическое выражение |
|---|---|
| Линейная функция | f(x) = ax + b, где a и b - константы |
| Квадратичная функция | f(x) = ax^2 + bx + c, где a, b и c - константы |
| Тригонометрическая функция | f(x) = sin(x) |
| Экспоненциальная функция | f(x) = e^x |
Аналитические функции позволяют проводить различные операции над ними, такие как вычисление производной, интеграла, нахождение точек перегиба и экстремумов и многое другое. Они являются основой для развития математического анализа и многих других разделов математики.
Понятие и основные свойства
Главное преимущество аналитически заданных функций заключается в их точности и простоте использования. Они позволяют выразить зависимость между переменными с высокой степенью точности и могут быть анализированы методами математического анализа.
Аналитически заданные функции могут иметь различные свойства, включая:
| Непрерывность | Функция непрерывна на интервале, если она может быть нарисована гладкой кривой без переломов и разрывов. |
| Дифференцируемость | Функция дифференцируема на интервале, если она имеет производную (скорость изменения функции) в каждой точке этого интервала. |
| Интегрируемость | Функция интегрируема на интервале, если существует определенный интеграл функции на этом интервале. |
| Монотонность | Функция монотонна на интервале, если она либо всегда возрастает, либо всегда убывает на этом интервале. |
Это лишь некоторые из основных свойств аналитически заданных функций. Зная свойства функций, мы можем более глубоко изучать их поведение и решать различные математические задачи с их помощью.
Примеры аналитически заданных функций:
Вот несколько примеров аналитически заданных функций:
- Линейная функция: f(x) = ax + b, где a и b - константы.
- Квадратичная функция: f(x) = ax^2 + bx + c, где a, b и c - константы.
- Синусоидальная функция: f(x) = a*sin(bx + c), где a, b и c - константы.
- Экспоненциальная функция: f(x) = a*e^(bx), где a и b - константы, и e - число Эйлера.
Эти примеры демонстрируют разнообразие аналитически заданных функций, которые могут быть использованы для моделирования и анализа различных явлений и процессов.
Полиномиальные функции
Примеры полиномиальных функций:
- Функция f(x) = 3x^2 - 2x + 1 является полиномиальной функцией, так как состоит из трех слагаемых, умноженных на степени переменной x.
- Функция g(x) = -5x^3 + 4x^2 - x является полиномиальной функцией, так как состоит из трех слагаемых, умноженных на степени переменной x.
- Функция h(x) = 7x^4 - 3x^3 + 2x^2 - x + 1 является полиномиальной функцией, так как состоит из пяти слагаемых, умноженных на степени переменной x.
Полиномиальные функции часто используются для моделирования различных явлений в науке, инженерии и экономике. Они обладают многими полезными свойствами, такими как возможность определения производных и интегралов, а также использование для нахождения корней уравнений.
Тригонометрические функции
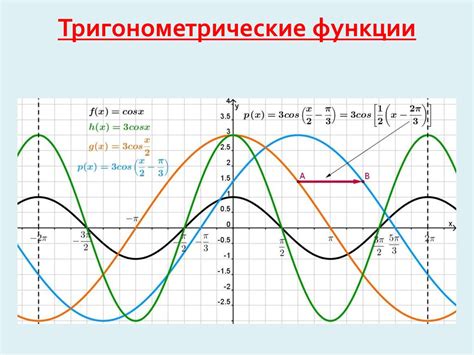
Основные тригонометрические функции включают синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc).
Синус (sin) угла в треугольнике определяется как отношение противолежащего катета к гипотенузе треугольника.
Косинус (cos) угла в треугольнике определяется как отношение прилежащего катета к гипотенузе треугольника.
Тангенс (tan) угла в треугольнике определяется как отношение противолежащего катета к прилежащему катету треугольника.
Котангенс (cot) угла в треугольнике определяется как обратное отношение тангенсу: cot = 1 / tan.
Секанс (sec) угла в треугольнике определяется как обратное отношение косинуса: sec = 1 / cos.
Косеканс (csc) угла в треугольнике определяется как обратное отношение синуса: csc = 1 / sin.
Тригонометрические функции используются в различных областях науки и техники, включая физику, инженерию и компьютерную графику.
Экспоненциальные и логарифмические функции
Логарифмическая функция – это обратная к экспоненциальной функции функция. Связь между экспоненциальной и логарифмической функциями выражается в следующем:
f(x) = a^x ↔ x = logaf(x)
То есть, если мы знаем значение экспоненциальной функции f(x) при известном значении аргумента x, мы можем найти соответствующий логарифм этого значения. Например, если f(x) = 8 при x = 3, то x = log28 = 3.
Для экспоненциальных функций с базой a > 1 график функции имеет форму восходящей кривой, а для a e, где e – основание натурального логарифма.
Логарифмические функции также имеют свои особенности. Например, график логарифма с базой a > 1 имеет характерный вид возрастающей кривой, график с базой a e является натуральным логарифмом и широко используется в математике и естественных науках.








