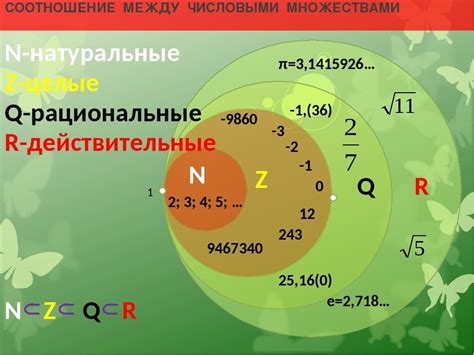
Числовые множества - это основа математики, которая изучает множества чисел и их свойства. Они представляют собой наборы чисел, объединенных определенными правилами. Каждое числовое множество имеет свои уникальные характеристики и значения, что делает его важным инструментом для анализа и решения различных математических задач.
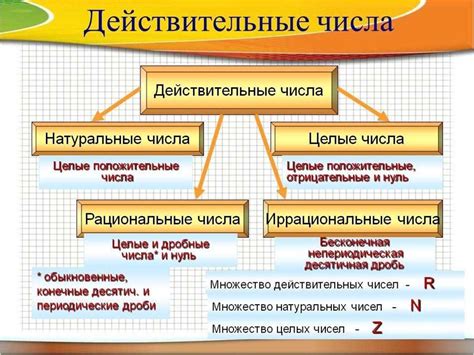
Основные понятия, используемые в числовых множествах, включают натуральные числа, целые числа, рациональные числа, иррациональные числа и действительные числа. Натуральные числа - это числа, которые используются для подсчета и упорядочивания объектов. Целые числа включают натуральные числа и их отрицания, что позволяет учитывать положительные и отрицательные значения. Рациональные числа представляются в виде дробей, где числитель и знаменатель являются целыми числами. Иррациональные числа - это числа, которые не могут быть представлены в виде дроби и имеют бесконечное количество десятичных разрядов.
Действительные числа объединяют все рациональные и иррациональные числа и представляют все возможные значения на числовой оси. Они включают в себя целые числа, десятичные дроби, корни и многое другое. Важно понимать, что числа могут быть элементами нескольких числовых множеств одновременно, что предоставляет гибкость для проведения различных операций и анализа данных.
Числовые множества находят широкое применение в различных областях науки и техники, таких как физика, экономика, компьютерная наука и другие. Понимание основных понятий числовых множеств и их значений позволяет ученым и инженерам более точно моделировать и анализировать реальные явления и процессы.
Натуральные числа и их свойства

Основные свойства натуральных чисел включают:
- Порядок: Натуральные числа имеют упорядоченную структуру, которая определяется их относительным значением. Например, число 3 следует после числа 2, а число 5 следует после числа 4. Это свойство является основой для операций сравнения и сортировки натуральных чисел.
- Сложение: Натуральные числа можно складывать между собой. Сложение двух натуральных чисел дает результат, также являющийся натуральным числом. Например, 2 + 3 = 5.
- Вычитание: Натуральные числа можно вычитать друг из друга. Однако вычитание может привести к отрицательному результату или нулю, что нарушает определение натуральных чисел. Поэтому вычитание в контексте натуральных чисел обычно определено только для ситуаций, когда результат является натуральным числом. Например, 5 - 2 = 3.
- Умножение: Натуральные числа можно умножать между собой. Умножение двух натуральных чисел дает результат, также являющийся натуральным числом. Например, 2 * 3 = 6.
- Деление: Натуральные числа можно делить друг на друга. Однако при делении возникает понятие остатка от деления. Если деление натуральных чисел нацело, то результат также является натуральным числом. Например, 6 / 2 = 3.
- Делители: Натуральное число называется делителем другого натурального числа, если это число делится нацело на данное. Например, делители числа 6 являются числа 1, 2, 3 и 6.
Натуральные числа имеют множество свойств и используются в различных областях математики, науки и повседневной жизни. Они служат основой для построения других числовых систем и выполняют важные функции в арифметических операциях и анализе данных.
Целые числа и их специфика
| Обозначение | Значение |
|---|---|
| ℤ | Множество всех целых чисел |
| ℤ+ | Множество положительных целых чисел, включая нуль |
| ℤ- | Множество отрицательных целых чисел, включая нуль |
Целые числа можно складывать, вычитать, умножать и делить. Они также поддерживают операции сравнения, такие как больше (>), меньше (
Примеры целых чисел:
- 0
- 1
- -5
Целые числа важны в программировании, физике, экономике и других областях науки. Они используются для представления количеств, координат, даты и времени, а также для решения различных задач и уравнений.
Рациональные числа и особенности их представления
Рациональные числа представляют собой числа, которые можно представить в виде отношения двух целых чисел: делимого (числителя) и делителя (знаменателя). Данный вид чисел включает в себя целые числа, десятичные дроби, обыкновенные дроби, а также проценты и пропорции.
Рациональные числа обозначаются обычно буквой Q (от англ. "quotient", что означает "частное"). Они являются одним из основных числовых множеств и включают в себя такие числа как 1, -5, 0, 0.25, 3/4, и т.д.
Представление рациональных чисел может осуществляться в различных форматах. Наиболее распространенной формой является обыкновенная дробь, где числитель и знаменатель являются целыми числами. Например, число 3/4 может быть представлено в виде обыкновенной дроби, где числитель равен 3, а знаменатель равен 4.
Еще одним способом представления рациональных чисел является десятичная дробь. В этом случае число представляется в виде десятичной дроби с ограниченным или бесконечным количеством знаков после запятой. Например, число 0.25 может быть записано как 0.25 или 0.2500 и т.д.
Кроме того, рациональные числа могут быть представлены в процентном виде, где число выражается в виде десятичной дроби, умноженной на 100 и с символом процента (%). Например, число 0.25 может быть представлено как 25%.
Рациональные числа обладают определенными особенностями, такими как возможность выполнить операции сложения, вычитания, умножения и деления, как с целыми числами, так и с другими рациональными числами. Однако при выполнении арифметических операций над рациональными числами может возникнуть потеря точности, особенно при работе с бесконечными десятичными дробями.
| Запись | Описание |
|---|---|
| 1/4 | Обыкновенная дробь |
| 0.25 | Десятичная дробь |
| 25% | Процентная форма |
Бесконечные и конечные десятичные дроби
Десятичная дробь может быть как конечной, так и бесконечной. Конечная десятичная дробь имеет ограниченное число знаков после запятой и может быть точно представлена в виде десятичной записи. Например, число 0,25 - конечная десятичная дробь, так как число знаков после запятой ограничено двумя.
Бесконечная десятичная дробь имеет бесконечное количество знаков после запятой и не может быть точно представлена в виде десятичной записи. Например, число π (пи) - бесконечная десятичная дробь, так как оно имеет бесконечное количество знаков после запятой.
Бесконечные десятичные дроби могут быть периодическими и непериодическими. Если десятичная дробь имеет повторяющийся блок знаков после запятой, она называется периодической. Например, число 1/3 (единица третья) имеет блок знаков "3" после запятой, который повторяется бесконечно, поэтому оно является периодической десятичной дробью.
Конечные и бесконечные десятичные дроби могут иметь разные значения, например, число 0,999... равно единице, хотя на первый взгляд может показаться, что оно меньше единицы.
Иррациональные числа: что они и почему они важны
Иррациональные числа играют важную роль в математике и науке. Они позволяют нам понять и описать некоторые естественные явления, такие как округление и приближение. Например, при вычислении площади круга или длины окружности, мы сталкиваемся с необходимостью использования иррационального числа π.
Иррациональные числа также встречаются в различных математических формулах и уравнениях. Они являются неотъемлемой частью алгебры, геометрии, физики и других наук. Большинство иррациональных чисел не могут быть представлены с помощью корней или других простых алгебраических выражений, поэтому они требуют особого подхода при их изучении и использовании.
Иррациональные числа также вызывают удивление и заинтересованность ученых и математиков. Они демонстрируют бесконечность и непредсказуемость математического мира. Многие иррациональные числа являются трансцендентными, то есть они не являются корнями никакого алгебраического уравнения. Это делает их еще более загадочными и привлекательными для изучения и исследования.
| Примеры иррациональных чисел: |
|---|
| √2 |
| √3 |
| √5 |
| π (пи) |
| e (основание натурального логарифма) |
Иррациональные числа являются важными и неотъемлемыми элементами математики, которые помогают нам понять и объяснить мир вокруг нас. Их исследование и использование в научных и практических приложениях продолжается, и они всегда будут занимать особое место в математическом пантеоне.








