Что значит укажите число обратное числу? Это выражение означает найти число, которое при умножении на данное число даёт единицу. Математически это выражается как "1 / x", где "x" - это данное число. Таким образом, обратное число является числом, результат умножения которого на данное число равен 1.
Обратное число можно найти как десятичную дробь или как десятичную дробь с бесконечными знаками после запятой. Например, для числа 2 обратное число будет 0.5, так как 2 * 0.5 = 1. Для числа 3 обратное число будет около 0.333333 и так далее.
Укажите число обратное числу может быть полезным при решении математических задач, а также в физике, экономике и других науках. Например, при расчёте вероятностей или при нахождении коэффициентов в уравнениях.
Следует помнить, что некоторые числа, например, ноль, не имеют обратного числа. По определению, деление на ноль не определено в математике, поэтому ноль не имеет обратного числа.
Описание понятия обратного числа

Обратное число представляет собой число, при умножении на которое данное число дает единицу.
Обратное число может быть найдено путем деления единицы на это число. Если число равно нулю, то его обратного числа не существует, так как деление на ноль запрещено.
Обратное число можно найти по формуле:
Обратное число = 1 / число
Примеры:
Для числа 2 обратное число будет: 1 / 2 = 0.5
Для числа -3 обратное число будет: 1 / -3 = -0.33
Обратное число является важным понятием в математике и используется в различных расчетах и уравнениях.
Что такое обратное число и как его найти
Чтобы найти обратное число, нужно разделить единицу на исходное число. Формула для нахождения обратного числа выглядит следующим образом:
Обратное число = 1 / исходное число
Например, пусть исходное число равно 4. Чтобы найти его обратное число, мы делим единицу на 4:
- Обратное число = 1 / 4 = 0.25 (четверть)
Таким образом, обратное число для числа 4 равно 0.25.
Если исходное число равно 0, то его обратного числа нет, так как невозможно разделить единицу на ноль.
Обратные числа имеют свойство, что произведение исходного числа и его обратного числа всегда равно единице:
- Исходное число * обратное число = 1
Понятие обратного числа и его значения

Например, обратное число к числу 4 будет равно 1/4 или 0.25. Если умножить 4 на 0.25, получим 1.
Обратные числа имеют следующие значения:
Обратное число к нулю не существует, так как нельзя поделить единицу на ноль.
Обратное число к единице равно самой единице: 1.
Обратное число к положительному числу будет положительным числом с дробной частью.
Обратное число к отрицательному числу будет отрицательным числом с дробной частью.
Например, обратные числа к 2 и -3 будут равны 1/2 и -1/3 соответственно.
Обратные числа являются важным понятием в математике и имеют множество применений в различных областях, включая физику, экономику и инженерию.
Примеры нахождения обратного числа
| Исходное число | Обратное число |
|---|---|
| 2 | 0.5 |
| 5 | 0.2 |
| 7 | 0.14285714285714285 |
Как видно из таблицы выше, обратное число отличается от исходного числа тем, что оно обратно пропорционально к нему. Чем больше исходное число, тем меньше его обратное число, и наоборот. Например, обратное число для числа 2 равно 0.5, а для числа 5 - 0.2.
Применение обратных чисел в математике
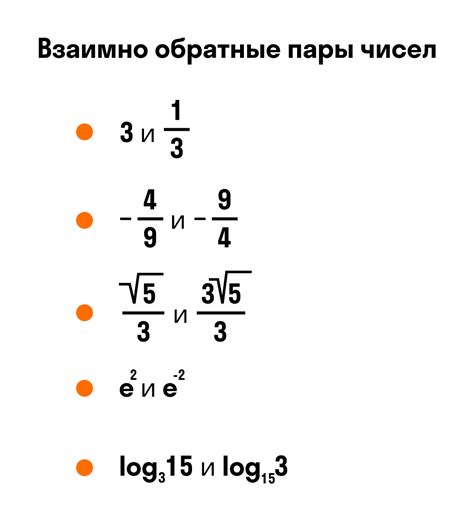
Для нахождения обратного числа следует выполнить следующую операцию: число необходимо разделить на единицу. Другими словами, обратное число можно получить, взяв его исходное значение и разделив его на единицу.
Например, обратное число для числа 2 будет 1/2 или 0,5, так как 2 * 0,5 = 1. Аналогично, обратное число для числа 5 будет 1/5 или 0,2, так как 5 * 0,2 = 1.
Обратные числа имеют важное значение в алгебре. Например, чтобы разделить одну дробь на другую, нужно умножить ее на обратную дробь. Также, обратные числа используются при вычислении производных в дифференциальном исчислении.
В заключение, обратные числа играют важную роль в математике. Они позволяют решать уравнения, упрощать дроби и проводить вычисления в различных областях математики.








