Решение неравенств - основной аспект алгебры и математики в целом. Неравенства могут быть линейными или квадратными, а их решения могут быть целыми или дробными числами. В данной статье мы обратимся к вопросу о том, как найти количество целых решений неравенств.
Количество целых решений неравенства зависит от его типа и формы записи. Например, линейные неравенства могут иметь бесконечное количество целых решений, если они записаны в виде "x ≥ a", где "a" - целое число. Квадратные неравенства могут иметь два, одно или ни одного целого решения в зависимости от дискриминанта и коэффициентов.
Для нахождения количества целых решений неравенства необходимо проанализировать условия, заданные в неравенстве, и определить допустимые значения переменных. Затем можно использовать методы алгебры и графики, чтобы найти количество целых решений.
Далее рассмотрим примеры различных типов неравенств и объясним, как найти количество их целых решений. Это поможет вам разобраться в этом важном аспекте математики и применить его на практике.
Что такое неравенство и как его решать?
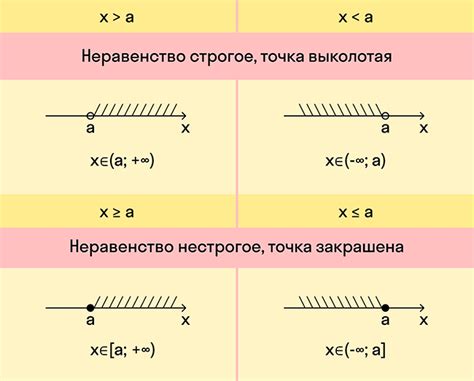
Для решения неравенств существует несколько методов, в зависимости от вида и сложности самого неравенства:
- Метод графика: позволяет представить неравенство в виде графика на координатной плоскости. Затем следует определить область, где выполнено условие неравенства.
- Метод приведения к квадратному уравнению: применяется в случае, когда неравенство содержит произведение переменных и не может быть решено простым сравнением значений.
- Метод подстановки: заключается в последовательной замене неизвестных переменных и проверке выполнения неравенства для каждой замены.
- Метод анализа знака: используется для неравенств, содержащих несколько выражений в одной переменной. После анализа знаков каждого выражения находятся интервалы, где выполняется неравенство.
Выбор метода решения неравенства зависит от конкретной задачи и сложности самого неравенства. Решив неравенство, можно найти его решения или промежуток, где оно выполняется. Это помогает определить область возможных значений для неизвестной переменной и использовать результаты в дальнейших вычислениях или задачах.
Как формализовать неравенство с целочисленными решениями?
Для начала, давайте определим, что такое формализация. Формализация означает превращение некоторой концепции или идеи в математическую структуру с использованием определенных правил и символов. Для формализации неравенств с целочисленными решениями мы используем нотацию, которая позволяет нам определить диапазон целых чисел, удовлетворяющих данному неравенству.
Одним из основных способов формализации неравенств является использование символа "" для указания направления неравенства. Например, неравенство "x > 5" означает, что значение переменной x должно быть больше 5. Если мы ищем целочисленные решения этого неравенства, то мы ищем все целые числа, которые больше 5.
Еще одним способом формализации неравенств с целочисленными решениями является использование символа "≥" или "≤" для указания направления неравенства. Например, неравенство "x ≥ 3" означает, что значение переменной x должно быть больше или равно 3. Если мы ищем целочисленные решения этого неравенства, то мы ищем все целые числа, которые больше или равны 3.
Как видно из примеров выше, формализация неравенств с целочисленными решениями позволяет нам точно определить множество целых чисел, которые удовлетворяют данному неравенству. Это может быть полезно при решении различных задач, где требуется найти все возможные значения переменных, удовлетворяющие заданным ограничениям.
| Неравенство | Формализация |
|---|---|
| x > 5 | x > 5 |
| x ≥ 3 | x ≥ 3 |
Как найти все целочисленные решения неравенства?

Во-первых, решаем неравенство как уравнение. Если у нас есть неравенство вида f(x) критические точки, при которых функции равны друг другу.
Во-вторых, анализируем неравенство в интервалах между критическими точками функций. Для этого берем произвольные значения из каждого интервала и проверяем их на выполнение условия неравенства. Нужно учесть, что если неравенство имеет строгий знак (), то на границах интервалов решений не будет.
Если имеются дополнительные ограничения на переменные в неравенстве, то мы должны рассматривать их вместе с условиями неравенства. Например, если переменная x должна быть положительной, то мы должны учесть это при нахождении решений.
Итак, чтобы найти все целочисленные решения неравенства, мы сначала решаем его как уравнение, находим критические точки, а затем анализируем интервалы между ними и дополнительные условия на переменные. Пошаговый подход поможет найти все возможные целочисленные решения и учесть все условия задачи.
Метод применения графиков для нахождения целых решений
Для применения этого метода требуется построить на плоскости график левой и правой частей неравенства. Затем необходимо определить область пересечения двух графиков, которая будет содержать все целочисленные значения, удовлетворяющие неравенству.
При помощи графиков можно определить количество целых решений неравенства, если область пересечения графиков имеет вид отрезка на числовой оси. В этом случае количество целых решений будет равно разности конечной и начальной точек отрезка плюс единица, так как отрезок включает в себя обе эти точки.
Пример:
| Неравенство: | x + 2 ≤ 5 |
| График левой части: | Прямая, проходящая через точки (-2, 0) и (0, 2) |
| График правой части: | Горизонтальная прямая y = 5 |
| Область пересечения: | Отрезок [3, 5] |
| Количество целых решений: | 3 |
Таким образом, в данном примере неравенство имеет три целых решения: 3, 4 и 5.
Как использовать алгоритмы для нахождения всех решений неравенства?

Для нахождения всех решений неравенства существует несколько алгоритмов, которые позволяют систематически перебирать все возможные значения переменных и определять, какие из них удовлетворяют заданному неравенству.
Один из таких алгоритмов - это метод перебора, при котором переменные пробуются последовательно с заданным шагом. В этом случае, если переменная удовлетворяет неравенству, она считается одним из решений. Таким образом, перебирая все значения переменных, мы можем найти все целые решения неравенства.
Другой алгоритм - это использование свойств и правил алгебры для преобразования неравенства в другую форму и последующего анализа. Например, для линейных неравенств применяются правила сложения, вычитания, умножения и деления для того, чтобы выразить переменную через константу и определить диапазон значений, в котором она может находиться.
Также существуют специальные алгоритмы для решения определенных видов неравенств, например, для квадратных или показательных неравенств. Эти алгоритмы позволяют находить все целые решения или классифицировать их по определенным критериям.
Более сложные неравенства могут требовать применения более сложных алгоритмов, таких как метод полного перебора или методы численного анализа. В таких случаях решение неравенства может быть получено с использованием компьютерных программ или специализированных математических программ.
Важно понимать, что каждый алгоритм имеет свои ограничения и может быть применим только к определенным типам неравенств. Поэтому важно учитывать особенности каждого конкретного неравенства и выбирать подходящий алгоритм для его решения.
Примеры нахождения количества целых решений неравенства
Для нахождения количества целых решений неравенства можно использовать различные методы, зависящие от вида неравенства.
Пример 1:
Исходное неравенство: 2x - 5 < 0
Решение:
1. Найдем точку, в которой выражение в неравенстве равно нулю: 2x - 5 = 0
2. Решим полученное уравнение и найдем значение переменной: x = 2.5
3. Построим числовую прямую и отметим найденную точку:
───•───────────
4. После этого проверим значения в интевалах, которые образовались на числовой прямой:
- Если значение между минус бесконечностью и 2.5, то удовлетворяет условию неравенства.
- Если значение больше 2.5, то не удовлетворяет условию неравенства.
В результате получаем, что решение неравенства 2x - 5 < 0 имеет бесконечное количество целых решений.
Пример 2:
Исходное неравенство: x2 - 4 ≥ 0
Решение:
1. Факторизуем выражение в левой части неравенства: (x - 2)(x + 2) ≥ 0
2. Найдем значения переменной, при которых выражение равно нулю: x = -2, x = 2
3. Построим числовую прямую и отметим найденные точки:
───•───────────•──────
4. После этого проверим значения в интервалах, образованных найденными точками:
- Если значение вне интервала (-бесконечность, -2) или (2, бесконечность), то удовлетворяет условию неравенства.
- Если значение попадает в интервал (-2, 2), то не удовлетворяет условию неравенства.
В результате получаем, что решение неравенства x2 - 4 ≥ 0 имеет два целых решения: x ≥ -2 и x ≤ 2.
Применение математических доказательств в задачах с целочисленными решениями

В математике доказательства играют важную роль для подтверждения или опровержения различных утверждений. Они позволяют строго и логически строить рассуждения, что особенно полезно при решении задач с целочисленными решениями неравенств. В этом разделе мы рассмотрим применение математических доказательств в таких задачах.
При решении задач с целочисленными решениями неравенств, основным шагом является установление условий, при которых существуют целочисленные решения.
Для примера рассмотрим неравенство: $x^2 + 7 > 3x$, где $x$ - целое число.
| Условия для решения | Целочисленные решения | |
|---|---|---|
| 1 | $3x - x^2 - 7 | $x \leq 2$ |
| 2 | $3x - x^2 - 7 > 0$ | $x \geq 3$ |
Из таблицы видно, что неравенство имеет целочисленные решения при $x \leq 2$ и $x \geq 3$. То есть, возможные целочисленные решения -2, -1, 0, 1, 2, 3, 4, 5, ...
Таким образом, математические доказательства позволяют строго установить условия для нахождения целочисленных решений неравенств. Они позволяют избежать неточных или неправильных решений и дают возможность получить аккуратный и простой ответ на задачу.
Особенности неравенств с одной переменной и несколькими переменными
Неравенства с одной переменной и несколькими переменными имеют свои особенности и требуют специального подхода к решению. Рассмотрим основные характеристики и методы решения таких неравенств.
Неравенства с одной переменной:
Когда уравнение содержит только одну переменную, решение можно представить в виде численного интервала. Для этого необходимо определить все значения переменной, при которых неравенство выполняется. В результате получится множество чисел, которое образует интервал на числовой прямой.
Например, неравенство x > 3 имеет решение в виде интервала (3, +∞), то есть все значения x больше 3.
Для решения неравенства с одной переменной может использоваться метод декартовых множеств или графический метод.
Неравенства с несколькими переменными:
Когда неравенство содержит несколько переменных, решение представляет собой область в многомерном пространстве. Для определения этой области необходимо описать ограничения на значения переменных, при которых неравенство выполняется.
Например, неравенство x + y > 5, x > 1, y > 2 имеет решение в виде области в плоскости координат, ограниченной линиями x + y = 5, x = 1 и y = 2.
Для решения неравенств с несколькими переменными может использоваться метод графиков или метод подстановки.
Округление и его роль в задачах на поиск количества целых решений

Округление имеет два основных типа: округление вверх и округление вниз. Округление вверх выполняется путем прибавления 0,5 и взятия целой части числа, что позволяет округлить число до ближайшего целого, большего или равного исходному числу. Округление вниз, с другой стороны, выполняется путем отбрасывания дробной части числа, что позволяет округлить число до ближайшего целого, меньшего или равного исходному числу.
В задачах на поиск количества целых решений неравенств округление играет важную роль. При оценке количества целых чисел, удовлетворяющих неравенству, мы можем использовать округление для определения границ, в которых могут находиться эти целые числа. Затем мы можем применить методы подсчета, чтобы определить точное количество целых решений.
Рассмотрим следующий пример:
| Задача | Неравенство |
|---|---|
| Пример 1 | x^2 - 2x + 1 |
Чтобы найти количество целых решений данного неравенства, мы можем воспользоваться округлением для определения границ, в которых может находиться целое число x. Первым шагом является решение квадратного трехчлена x^2 - 2x + 1 = 0. Заметим, что данное уравнение имеет единственное решение x = 1. Это означает, что неравенство может выполниться только в интервалах, где x 1.
Для определения количества целых решений неравенства, мы можем воспользоваться методом подсчета. В данном случае, так как неравенство левостороннее, мы можем начать с числа x = 0 и перебирать все целые числа в отрицательном направлении, пока неравенство не перестанет выполняться. Затем делаем то же самое в положительном направлении, начиная с x = 2. Количество целых решений будет равно сумме количества целых чисел в каждом интервале.
В данном случае неравенство x^2 - 2x + 1
Таким образом, округление является важным инструментом при решении задач на поиск количества целых решений неравенств. Оно позволяет нам определить границы, в которых находятся целые числа, и применить методы подсчета для определения точного количества целых решений.








