Четность и нечетность функции — это важные понятия в математике, которые помогают понять ее особенности и свойства. Они обозначают свойства функции, которые проявляются при изменении аргумента. В данной статье рассмотрим, что такое четная и нечетная функция, как их определить и какие особенности у них есть.
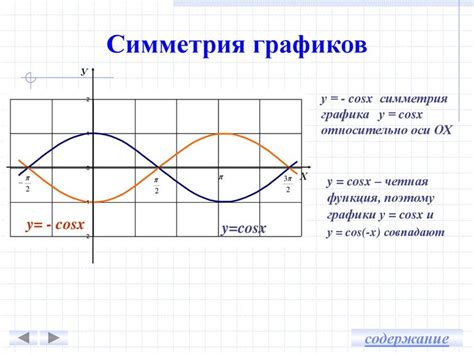
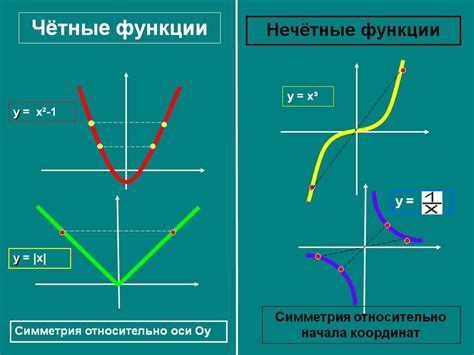
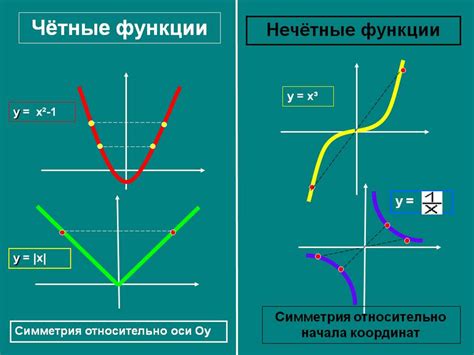
Четная функция определяется таким образом, что для любого значения аргумента x выполняется условие f(-x) = f(x). Это значит, что значения функции симметричны относительно оси ординат. Визуально это выражается в следующем: график четной функции симметричен относительно оси ординат. Примерами четных функций являются функция y = x^2 и функция y = |x|.
Нечетная функция определяется таким образом, что для любого значения аргумента x выполняется условие f(-x) = -f(x). Это значит, что значения функции симметричны относительно начала координат. Визуально это выражается в следующем: график нечетной функции симметричен относительно начала координат. Примерами нечетных функций являются функция y = x^3 и функция y = sin(x).
Важно отметить, что функция может быть и четной, и нечетной одновременно. В этом случае говорят о четно-нечетной функции. Примером такой функции является функция y = x^4.
Четность и нечетность функции являются важными свойствами, которые позволяют упростить анализ функций и находить их симметричные относительно оси или начала координат части. Они активно используются в различных математических и научных приложениях для решения задач и построения моделей.
Определение четности функции
Функция является четной, если для любого значения аргумента x выполняется условие: f(x) = f(-x). То есть, если исходная функция при смене знака аргумента сохраняет своё значение.
Соответственно, функция является нечетной, если для каждого значения аргумента x выполняется условие: f(x) = -f(-x). То есть, если исходная функция при смене знака аргумента меняет своё значение на противоположное.
Зная свойства четности и нечетности функции, можно сделать выводы о симметрии её графика. Если функция является четной, то её график будет симметричен относительно оси ординат. Если функция является нечетной, то её график будет симметричен относительно начала координат.
Понятие и особенности четности и нечетности
Функция называется четной, если она обладает следующим свойством: при замене аргумента x на –x значение функции не меняется. Формально, функция f(x) называется четной, если f(-x) = f(x) для всех значений x из области определения функции.
Например, функция y = x^2 является четной, так как значение функции остается неизменным при замене x на –x: (-x)^2 = x^2.
Функция называется нечетной, если она обладает следующим свойством: при замене аргумента x на –x значение функции изменяется только по знаку. Формально, функция f(x) называется нечетной, если f(-x) = -f(x) для всех значений x из области определения функции.
Например, функция y = x^3 является нечетной, так как значение функции меняется только по знаку при замене x на –x: (-x)^3 = -(x^3).
Четные функции обладают симметрией относительно оси y, то есть их графики симметричны относительно оси y. Нечетные функции не обладают симметрией относительно оси y, но обладают симметрией относительно начала координат.
Четность и нечетность функций являются важными свойствами, которые позволяют упростить анализ функций и изучение их графиков. Эти свойства также применяются при решении различных задач в математике и других науках.
| Свойство | Четные функции | Нечетные функции |
|---|---|---|
| Поведение при замене x на –x | Значение функции не меняется | Значение функции меняется по знаку |
| Графическая симметрия | Симметричны относительно оси y | Симметричны относительно начала координат |
Алгебраический и графический подходы к определению четности

Определение четности функции можно выполнить как с помощью алгебраического, так и графического подхода.
Алгебраический подход основан на изучении свойств функции и ее алгебраической записи. Для определения четности функции необходимо проверить, сохраняются ли значения функции при подстановке x или -x. Если значения сохраняются при замене x на -x, то функция является четной. Если значения меняются при такой замене, то функция является нечетной.
Графический подход заключается в анализе графика функции. Четная функция обладает симметрией относительно оси ординат, то есть график функции симметричен относительно оси y. Нечетная функция же обладает симметрией относительно начала координат (точки (0,0)), то есть график функции симметричен относительно начала координат.
По графическому подходу можно определить четность функции путем проверки симметрии графика при изменении аргумента x на -x. Если график не меняется при смене знака аргумента, то функция является четной. Если же график изменяется, то функция является нечетной.
Способы определения четности и нечетности функций
1. Метод подстановки:
Для определения четности и нечетности функции можно использовать метод подстановки. Для этого необходимо заменить переменную в функции на ее противоположную, а затем сравнить полученное выражение с исходной функцией.
Если функция сохраняет свое значение после замены переменной на противоположную, то она является четной. Если значение функции меняется со знаком на противоположный, то функция является нечетной.
2. Анализ графика функции:
Другим способом определения четности и нечетности функции является анализ ее графика. Если график функции симметричен относительно оси ординат, то функция является четной. Если график функции симметричен относительно начала координат, то функция является нечетной.
3. Использование алгебраических свойств:
Некоторые алгебраические свойства могут помочь определить четность или нечетность функции без необходимости в подстановке или анализе графика. Например, для определения четности или нечетности функции можно использовать следующие свойства:
- Если функция является суммой или разностью двух функций, то ее четность или нечетность зависят от четности или нечетности этих функций.
- Если функция является произведением двух функций, то ее четность или нечетность зависят от суммы степеней четности или нечетности этих функций.
- Если функция является четной или нечетной, то ее степень также является четной или нечетной.
- Если функция является нечетной, то ее обратная функция также является нечетной.
Все эти способы позволяют определить четность или нечетность функции и использовать данную информацию при дальнейшем анализе и решении математических задач.
Определение четности и нечетности для элементарных функций
Часто при анализе функций возникает необходимость определить их четность или нечетность. Это позволяет упростить решение задач и понять особенности поведения функций.
Определение четности и нечетности основано на свойствах функции относительно оси абсцисс (ось X). Функция f(x) называется четной, если для любого значения x из области определения выполняется равенство f(x) = f(-x). Иными словами, график функции симметричен относительно оси Y.
Функция f(x) называется нечетной, если для любого значения x из области определения выполняется равенство f(x) = -f(-x). Иными словами, график функции симметричен относительно начала координат.
Определение четности и нечетности применяется не только к сложным функциям, но и к элементарным функциям. Например:
- Функция f(x) = xn, где n - целое число, четна при n четном и нечетна при n нечетном.
- Функция f(x) = sin(x) является нечетной.
- Функция f(x) = cos(x) является четной.
- Функция f(x) = tan(x) является нечетной.
Определение четности и нечетности позволяет проводить анализ функций, находить их симметричные точки и упрощать вычисления. Знание свойств четности и нечетности функций является важным инструментом в математике и ее приложениях.
Соотношение между четностью и нечетностью
Нечетная функция, наоборот, обладает осевой симметрией относительно начала координат. Значение функции для аргумента x равно противоположному значению для аргумента -x. Например, функция f(x) = x^3 является нечетной.
Существует также класс функций, которые не являются ни четными, ни нечетными. Они не обладают никакой осевой симметрией и могут иметь самые различные формы. Например, функция f(x) = x^5 + x^2 + 1.
Можно заметить, что произведение четной функции на четную функцию всегда даёт четную функцию. Аналогично, произведение нечетной функции на нечетную функцию всегда даёт четную функцию. В то же время, произведение четной функции на нечетную функцию всегда даёт нечетную функцию.
Эти особенности четности и нечетности функций позволяют упростить решение некоторых задач и определить четность или нечетность функции без подробных вычислений.
Примеры определения четности и нечетности функций
Ниже приведены примеры определения четности и нечетности функций:
| Функция | Определение | Четность | Нечетность |
|---|---|---|---|
| f(x) = x^2 | Подставим -x вместо x и сравним с исходной функцией: | f(-x) = (-x)^2 = x^2 = f(x) | Функция является четной, так как f(-x) = f(x) |
| g(x) = x^3 | Подставим -x вместо x и сравним с исходной функцией: | g(-x) = (-x)^3 = -x^3 = -g(x) | Функция является нечетной, так как g(-x) = -g(x) |
| h(x) = x^4 - x^2 | Подставим -x вместо x и сравним с исходной функцией: | h(-x) = (-x)^4 - (-x)^2 = x^4 - x^2 = h(x) | Функция является четной, так как h(-x) = h(x) |
Это лишь небольшая часть примеров определения четности и нечетности функций. При исследовании функций следует учитывать различные математические свойства и применять соответствующие методы для определения их четности или нечетности.
Практическое применение определения четности функции
Одним из практических применений определения четности функции является определение симметричности графика функции относительно оси ординат. Если функция является четной, то ее график симметричен относительно оси ординат. Если функция является нечетной, то ее график симметричен относительно начала координат. Это позволяет просто и быстро визуально определить симметричность графика функции без использования дополнительных инструментов.
Кроме того, знание о четности или нечетности функции позволяет упростить алгебраические вычисления. Например, для четной функции, интеграл по симметричному отрезку можно заменить на удвоенный интеграл по положительной полуоси. Аналогично, для нечетной функции, интеграл по симметричному отрезку будет равен нулю. Это позволяет сэкономить время и усилия при решении задач, связанных с определенными интегралами.
Еще одним применением определения четности функции является поиск симметричных точек графика. Для четных функций, если у нас есть точка на графики с координатами (x, y), то точка с координатами (-x, y) также будет лежать на графике. Аналогично, для нечетных функций, если у нас есть точка на графике с координатами (x, y), то точка с координатами (-x, -y) также будет лежать на графике. Это позволяет быстро находить парные точки на графике функции.
Все эти примеры демонстрируют практическую пользу от знания о четности или нечетности функции. Определение четности функции является важным инструментом в математике, который помогает анализировать и использовать функции в различных практических ситуациях.
Свойства и теоремы, связанные с четностью и нечетностью

Симметрия относительно оси OY: Если функция f(-x) = -f(x) для всех значения x из области определения функции, то она называется нечетной. То есть, график функции симметричен относительно оси OY.
Симметрия относительно начала координат: Если функция f(-x) = f(x) для всех значения x из области определения функции, то она называется четной. То есть, график функции симметричен относительно начала координат.
Сумма четной и нечетной функций: Сумма четной и нечетной функций всегда является нечетной функцией.
Произведение четной и нечетной функций: Произведение четной и нечетной функций всегда является четной функцией.
Определение нечетности через интеграл: Функция f(x) является нечетной, если интеграл от f(x) на симметричном отрезке [-a, a] равен нулю.








