Системы неравенств являются одним из фундаментальных понятий в математике и находят применение в различных практических областях. В основе систем неравенств лежит задача нахождения таких значений переменных, при которых все неравенства выполняются одновременно. Одним из вариантов таких решений являются целые числа. Это значит, что мы ищем целочисленные значения переменных, удовлетворяющие всем неравенствам системы.
Концепция целых решений в системах неравенств важна не только с теоретической точки зрения, но и имеет практическое применение. Примеры задач, в которых используются целые решения, включают планирование производства, оптимизацию логистических схем, анализ социально-экономических явлений и другие области. Также, целые решения могут использоваться в криптографии для решения различных задач безопасности.
Важно отметить, что поиск целых решений в системах неравенств является нетривиальной задачей, требующей использования специальных методов и алгоритмов. Однако, нахождение целых решений может привести к значительному упрощению и оптимизации решения задачи в сравнении с общими решениями.
В данной статье мы рассмотрим основы понятия целых решений в системах неравенств, рассмотрим основные методы и алгоритмы для их поиска, а также представим несколько примеров задач, в которых использование целых решений является наиболее эффективным подходом.
Понятие целых решений в системах неравенств

Система неравенств - это набор математических неравенств, содержащих переменные. Целые решения системы неравенств - это значения переменных, которые удовлетворяют всем неравенствам системы и являются целыми числами.
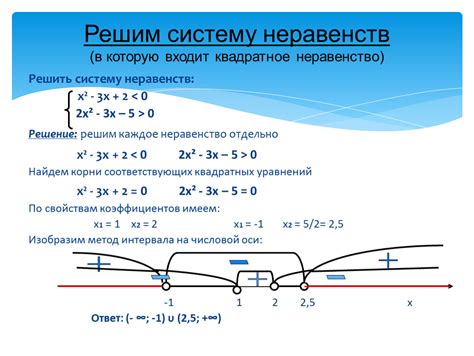
Для примера рассмотрим систему неравенств:
2x + 3y ≥ 10
x - y ≤ 5
Чтобы найти целые решения этой системы, необходимо проверить все возможные значения переменных, удовлетворяющие условиям.
В данном случае, можно начать проверять значения для переменной x от -∞ до +∞, а для переменной y от -∞ до +∞. Если находится целое значение, которое удовлетворяет обоим неравенствам, оно является целым решением системы.
Найденные целые решения могут быть представлены в виде пар чисел, например: (-1, 2), (2, 3), (-2, 4), и так далее.
Иногда системы неравенств имеют бесконечное количество целых решений. В таких случаях, записывают общую формулу для решений, указывая условия, которые должны удовлетворяться.
Определение и сущность целых решений
Целые решения в системах неравенств представляют собой такие значения неизвестных, при которых все неравенства системы выполняются при помощи целых чисел. Такие решения могут быть представлены в виде упорядоченных пар или кортежей целых чисел.
Основная сущность целых решений заключается в нахождении множества всех возможных значений неизвестных, при которых выполняются все заданные неравенства. Целые решения могут иметь как конечное, так и бесконечное множество значений. Они играют важную роль в различных областях математики, физики и экономики, где требуется нахождение целочисленных решений для построения моделей или принятия решений.
Для нахождения целых решений в системах неравенств применяются различные методы, такие как метод перебора, метод отсечений и другие алгоритмы с использованием дискретной математики. При решении систем неравенств с целыми значениями необходимо учитывать возможные ограничения и условия, такие как диапазон значений, ограничения на переменные и т.д.
Знание и понимание целых решений и их сущности играют важную роль в решении различных задач оптимизации, моделирования и принятия решений. Целые решения позволяют найти оптимальные значения переменных при условии соблюдения заданных неравенств и ограничений. Поэтому изучение и практическое применение целых решений являются важным аспектом при решении различных задач в различных сферах деятельности.
Математические основы систем неравенств
Решением системы неравенств является множество точек на плоскости или в пространстве, которые удовлетворяют всем неравенствам системы. Такое множество может быть представлено в качестве графика или списком координат.
Для определения решений системы неравенств можно использовать метод графического представления. В этом случае каждое неравенство из системы представляется на графике в виде линии или плоскости, а решение системы - это область пересечения или объединения всех таких линий или плоскостей.
Также существуют методы алгебраического исследования систем неравенств. Например, можно привести систему неравенств к более простой форме, применив к ней алгебраические преобразования. Или можно использовать метод подстановки, замещая переменные из одной неравенства в другие и получая тем самым новые неравенства.
Решение системы неравенств может быть ограничено или неограничено. Если решение системы состоит из конечного количества точек, то оно считается ограниченным. Если же решение системы образует линию, плоскость или пространство, то оно считается неограниченным.
Понятие целых решений в системах неравенств связано с условием, что все переменные должны принимать только целочисленные значения. Такие системы называются диофантовыми системами неравенств. В таких системах можно искать только решения, в которых все переменные являются целыми числами.
Примеры систем неравенств
Пример 1:
Рассмотрим систему неравенств:
x + y > 5
x - y < 2
Данная система состоит из двух неравенств, где переменные x и y являются неизвестными. Чтобы найти множество всех решений этой системы, нужно определить такие значения x и y, при которых оба неравенства будут выполняться одновременно.
Пример 2:
Рассмотрим систему неравенств:
3x - 2y ≥ 6
x + 4y ≤ 10
В данном случае переменные x и y являются неизвестными. Чтобы найти множество всех решений системы неравенств, нужно определить такие значения x и y, при которых оба неравенства будут выполняться одновременно.
Пример 3:
Рассмотрим систему неравенств:
2x + y ≤ 8
x - y > 1
x > 0
В данном случае система состоит из трех неравенств, где переменные x и y являются неизвестными. Чтобы найти множество всех решений этой системы, нужно определить такие значения x и y, при которых все три неравенства будут выполняться одновременно.
Способы решения систем неравенств
Существуют различные подходы и методы для решения систем неравенств. В зависимости от сложности системы и требуемой точности решения, можно выбирать наиболее подходящий метод.
Ниже приведены некоторые из самых распространенных способов решения систем неравенств:
- Метод графиков
- Метод подстановки
- Метод исключения
- Метод дополнительных переменных
- Метод штрафных функций
При использовании этого метода решения системы неравенств каждое уравнение из системы представляется в виде графика на координатной плоскости. Пересечение графиков определяет точку, которая удовлетворяет всем неравенствам системы.
Метод подстановки заключается в том, чтобы выразить одну переменную через другую из одного из уравнений системы, а затем подставить это выражение в оставшиеся уравнения. Путем последовательной подстановки можно найти значения переменных, удовлетворяющие всем неравенствам.
Метод исключения основан на идее исключения переменных из системы неравенств. Для этого необходимо выразить одну переменную через другую из одного из уравнений, а затем это выражение подставить в другие уравнения. Операции исключения позволяют систематически избавиться от переменных и получить значения, удовлетворяющие системе.
Метод дополнительных переменных заключается в том, чтобы ввести дополнительные переменные, которые помогут упростить систему неравенств и получить более явное решение. Эти дополнительные переменные могут быть выбраны таким образом, чтобы неравенства стали более простыми для решения.
Метод штрафных функций заключается в том, чтобы добавить штрафные члены к каждому неравенству в системе и превратить задачу в оптимизационную задачу. Затем можно использовать различные алгоритмы оптимизации для поиска минимума штрафной функции, что приведет к определению решения системы.
Выбор метода решения системы неравенств зависит от ее особенностей, доступных ресурсов вычислительной техники и нужной точности решения. Зная основные методы, можно подобрать наиболее подходящий при решении конкретной задачи.
Ограничения и условия целых решений
Ограничения и условия целых решений могут быть выражены различными способами. Одним из распространенных способов является задание верхней или нижней границы для каждой переменной в системе неравенств. Например, система может иметь ограничения вида:
x ≥ 0
y ≤ 10
где x и y - переменные системы.
Другими ограничениями могут быть условия, связывающие значения переменных. Например, система может иметь ограничение вида:
x + y ≤ 15
где x и y - переменные системы.
Ограничения и условия могут быть заданы как неравенствами, так и равенствами. Они могут быть линейными или нелинейными. Ограничения также могут быть комбинацией различных типов неравенств. Целые решения системы неравенств должны удовлетворять всем ограничениям и условиям, заданным в системе.
Ограничения и условия целых решений играют важную роль в решении реальных задач. Например, при оптимизации процессов производства или распределении ресурсов может потребоваться найти множество целых значений переменных, удовлетворяющих определенным условиям. Понимание и умение работать с ограничениями и условиями целых решений является важным навыком в различных областях науки и прикладной математики.
Практическое применение целых решений

Понятие целых решений в системах неравенств широко применяется в различных областях науки и инженерии. Оно позволяет определить наборы целочисленных значений переменных, которые удовлетворяют определенным условиям.
Одной из областей, где целые решения находят применение, является оптимизация. Используя целые решения, можно найти наилучшее решение задачи с ограничениями на значения переменных. Например, в задаче распределения ресурсов можно использовать целые решения для определения наиболее эффективного распределения, учитывая ограничения на доступные ресурсы.
Еще одной областью, где находят применение целые решения, является теория игр. В играх с неполной информацией или с ограничениями на возможные ходы, можно использовать целые решения для определения наиболее выгодных стратегий. Целые решения позволяют рассматривать все возможные варианты и выбрать оптимальный.
Целые решения также находят применение в логистике и планировании. Например, при оптимизации пути доставки грузов можно использовать целые решения для определения наименьших затрат или наименьшего времени доставки. При планировании производства целые решения могут помочь оптимизировать распределение ресурсов и времени.
Все эти примеры показывают, что понятие целых решений в системах неравенств имеет широкое практическое применение и позволяет решать различные оптимизационные и планировочные задачи.
Альтернативные методы решения систем неравенств
Кроме классического метода решения систем неравенств, существуют и альтернативные подходы, которые могут быть эффективными в определенных случаях.
Один из таких методов - графическое решение системы неравенств. Для этого необходимо построить графики каждого уравнения в системе и определить область, где все графики пересекаются. Эта область будет содержать решения системы неравенств.
Еще одним альтернативным методом является метод подстановки. Он заключается в том, чтобы решить одно уравнение и подставить его решение во все остальные уравнения системы. Таким образом, можно получить значения переменных, удовлетворяющие всем уравнениям системы.
Также можно использовать метод исключения. Он предполагает последовательное исключение одной переменной из всех уравнений системы с помощью преобразований, пока не останется только одно уравнение с одной переменной. Затем это уравнение может быть решено, а найденное значение переменной подставлено в остальные уравнения для получения полных решений системы.
Альтернативные методы решения систем неравенств могут быть полезны в разных ситуациях, и их выбор зависит от конкретной системы и передаваемой задачи.








