Гиперболой называют геометрическую фигуру, которая представляет собой график уравнения вида y = a/x или x = a/y, где a - некоторое положительное число. Гипербола отличается от эллипса и параболы своей специфической формой и свойствами.
Одним из важных свойств гиперболы является наличие асимптот. Асимптотой гиперболы называется прямая, которая приближается к гиперболе при стремлении значений x или y к бесконечности. Асимптоты играют значимую роль в аналитической геометрии и имеют некоторые интересные свойства, которые стоит рассмотреть.
Первое свойство асимптот гиперболы - это их парные характеристики. Гипербола имеет две асимптоты, проходящие через центр координат и расположенные симметрично относительно осей координат. Это означает, что уравнения этих асимптот имеют вид y = kx и y = -kx, где k - параметр, связанный с коэффициентами уравнения гиперболы.
Определение и основные понятия
Асимптоты гиперболы – это прямые линии, которые подходят к гиперболе бесконечно близко, но никогда не пересекают ее. Асимптоты гиперболы имеют особые свойства: они параллельны друг другу и пересекаются в бесконечности.
Асимптоты гиперболы определяют ее форму и направление. Из уравнения асимптот гиперболы можно определить координаты вершин, фокусы и другие характеристики гиперболы.
Гипербола имеет две асимптоты: горизонтальную и вертикальную. Горизонтальная асимптота проходит через центр гиперболы и ординату (0, b). Вертикальная асимптота проходит через центр гиперболы и абсциссу (a, 0).
Уравнение гиперболы и его свойства
Уравнение гиперболы имеет следующий вид:
(x - h)²/a² - (y - k)²/b² = 1
Здесь (h, k) – координаты центра гиперболы, а a и b – полуоси гиперболы и соответственно определяют удаление фокусов от центра. При этом a больше b.
Некоторые основные свойства гиперболы:
| 1. | Гипербола состоит из двух отдельных ветвей. |
| 2. | Оси симметрии гиперболы проходят через ее центр. |
| 3. | Уравнение асимптот гиперболы имеет вид y = ±(b/a)x, где b и a – полуоси гиперболы. |
| 4. | Асимптоты гиперболы являются прямыми, к которым гипербола стремится при удалении от центра. |
| 5. | Гипербола имеет фокусы, которые находятся на оси симметрии и равноудалены от центра гиперболы. |
Фокусы и директрисы гиперболы
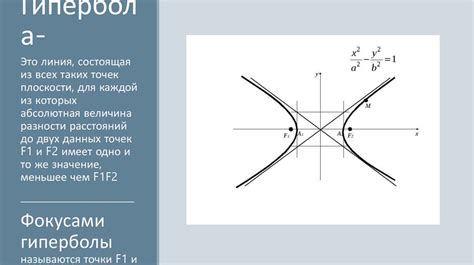
Фокусы гиперболы – это две точки, которые характеризуются особым свойством. Для каждой точки на гиперболе выполнено, что разность расстояний от этой точки до фокусов равна постоянному значению, называемому фокусным расстоянием. Фокусное расстояние обозначается буквой c. Фокусы гиперболы находятся на главной оси гиперболы и отделены от центра гиперболы на фокусное расстояние c.
Директрисы гиперболы – это две прямые, которые также связаны с особым свойством этой геометрической фигуры. Для каждой точки на гиперболе выполнено, что отношение расстояния от этой точки до директрисы к расстоянию от этой точки до фокусов равно постоянному значению, обозначаемому буквой ε (эпсилон) и называемому эксцентриситетом. Эпсилон лежит в диапазоне от 0 до 1, и чем меньше его значение, тем более "вытянутой" будет гипербола.
Директрисы гиперболы находятся на главной оси гиперболы и отличаются от фокусов на постоянное значение, зависящее от эксцентриситета ε. Формула для определения директрис в зависимости от эксцентриситета: директрисы равны ±a/ε, где a - полуось гиперболы, расположенная на главной оси.
Фокусы и директрисы гиперболы являются важными элементами этой геометрической фигуры и определяют ее форму и свойства. Они также используются для построения гиперболы на графике и в решении геометрических задач, связанных с этой кривой.
Уравнение асимптот гиперболы
- Асимптоты пересекаются в центре гиперболы.
- Угол между асимптотами равен углу, образуемому ветвями гиперболы.
- Асимптоты являются симметричными относительно центра гиперболы.
Уравнение асимптот гиперболы задается следующим образом:
Уравнение асимптоты I: y = mx + b
Уравнение асимптоты II: y = -mx + b
где m - коэффициент наклона асимптот, а b - смещение асимптоты по оси ординат.
Зная коэффициенты m и b, можно найти уравнения асимптот гиперболы и изучить их свойства.
Симметрия гиперболы относительно асимптот

Также гипербола симметрична относительно каждой из своих асимптот. Это означает, что при замене координат (x, y) на (-x, y) или (x, -y) уравнение гиперболы остается неизменным. Таким образом, гипербола симметрична относительно осей симметрии, которые проходят через ее асимптоты.
Из свойства симметрии гиперболы относительно асимптоты следует, что если точка P(x, y) лежит на гиперболе, то точка Q(-x, -y) также будет лежать на гиперболе. Это свойство можно использовать для построения графика гиперболы, если известны лишь несколько точек.
Построение графика гиперболы и ее асимптот
Для построения графика гиперболы и определения ее асимптот необходимо знать уравнение гиперболы вида:
(x - a)2 / (p2) - (y - b)2 / (q2) = 1
где a и b - координаты центра гиперболы, p и q - полуоси гиперболы.
График гиперболы можно построить следующим образом:
- Найти координаты центра гиперболы (a, b).
- Найти полуоси гиперболы (p, q).
- Найти координаты вершин гиперболы, которые равны (a ± p, b).
- Нарисовать вертикальные асимптоты, проходящие через вершины гиперболы.
- Нарисовать горизонтальные асимптоты, проходящие через центр гиперболы.
- Провести гиперболу, так чтобы ее график асимптотически стремился к вертикальным и горизонтальным асимптотам на бесконечности.
Асимптоты гиперболы являются прямыми, к которым график гиперболы стремится на бесконечности. Вертикальные асимптоты гиперболы имеют уравнение x = a ± p, а горизонтальные асимптоты - уравнение y = b.
Построение графика гиперболы позволяет визуализировать ее форму и определить поведение функции в окрестности асимптот. Знание асимптот гиперболы помогает анализировать асимптотическое поведение функции и решать задачи, связанные с гиперболами.
Взаимное расположение гиперболы и ее асимптот

Гипербола имеет две асимптоты, которые проходят через центр графика и симметрично относительно его осей. Асимптоты гиперболы имеют уравнения вида y = kx + b и y = -kx + b, где k - коэффициент наклона асимптоты, а b - некоторая константа. Значение k определяется коэффициентами уравнения гиперболы.
Важно отметить, что асимптоты гиперболы не пересекаются с графиком гиперболы, но они стремятся к нему бесконечно близко. В точках пересечения асимптот с гиперболой, график гиперболы может быть касательной к асимптоте.
Как правило, гипербола располагается между своими асимптотами. Левая и правая ветви гиперболы находятся внутри области, ограниченной ее асимптотами. Также, гипербола может иметь точки, которые лежат на ее асимптотах, но они не являются частью графика гиперболы.
Исследование взаимного расположения гиперболы и ее асимптот является важной задачей, которая позволяет лучше понять геометрические свойства гиперболы и использовать их для решения различных задач в математике и физике.
Использование асимптот гиперболы в математических моделях
Асимптоты гиперболы представляют собой важный элемент в построении математических моделей. Их использование позволяет получить приближенное представление гиперболической функции и улучшить точность результатов.
Одним из применений асимптот гиперболы является построение асимптотических разложений. Асимптотическое разложение – это представление функции в виде суммы бесконечного ряда, в котором каждый член является асимптотой к соответствующему слагаемому исходной функции. Это позволяет аппроксимировать функцию с любой заданной точностью.
Также асимптоты гиперболы используются при нахождении асимптотических оценок. Асимптотическая оценка – это представление функции в виде выражения, которое служит для оценки поведения функции при стремлении аргумента к определенной точке. Асимптотические оценки позволяют получить приближенное представление функции в окрестности заданной точки и упростить процесс решения математических задач.
Кроме того, асимптоты гиперболы используются в построении графиков функций. При построении графика гиперболической функции, асимптоты позволяют определить направление стремления к бесконечности и поведение функции в бесконечно удаленных точках.
Таким образом, асимптоты гиперболы играют важную роль в математических моделях, позволяя упростить решение задач, получить приближенные представления функций и определить их поведение в различных точках.
Примеры задач и решений, связанных с асимптотами гиперболы

Рассмотрим несколько примеров задач, связанных с асимптотами гиперболы, и их решений.
Пример 1:
Найдите уравнение асимптоты гиперболы с уравнением x^2/25 - y^2/9 = 1.
Решение:
Уравнение гиперболы имеет вид x^2/a^2 - y^2/b^2 = 1, где a и b - полуоси гиперболы. Из данного уравнения видно, что a = 5 и b = 3.
Так как гипербола симметрична относительно осей координат, асимптоты гиперболы проходят через центр, который находится в начале координат. Зная, что угловой коэффициент асимптоты равен ±(b/a), получаем, что уравнение асимптоты имеет вид y = ±(3/5)x.
Пример 2:
Определите положение гиперболы x^2/16 - y^2/9 = 1 относительно своих асимптот.
Решение:
В данном случае имеем a = 4 и b = 3. Угловые коэффициенты асимптот равны ±(b/a) = ±(3/4).
Асимптоты имеют уравнение y = ±(3/4)x. Чтобы определить положение гиперболы относительно асимптот, нужно сравнить уравнение гиперболы и уравнение асимптот в пределах бесконечности.
Если гипербола находится ниже асимптоты в пределах бесконечности, то она будет лежать внутри асимптот. Если гипербола находится выше асимптоты в пределах бесконечности, то она будет лежать между асимптотами.
В данном случае, так как уравнение гиперболы y = ±√(9x^2/16 - 9), видно, что y всегда меньше значений, определенных уравнением асимптот y = ±(3/4)x в пределах бесконечности. Значит, гипербола находится внутри асимптот и не пересекает их.
Пример 3:
Найдите фокусное расстояние и эксцентриситет гиперболы с уравнением x^2/9 - y^2/16 = 1.
Решение:
Для гиперболы с уравнением x^2/a^2 - y^2/b^2 = 1, фокусное расстояние вычисляется как c = √(a^2 + b^2), а эксцентриситет вычисляется как e = c/a.
В данном случае, имеем a = 3 и b = 4. Вычисляем фокусное расстояние: c = √(3^2 + 4^2) = 5. Затем вычисляем эксцентриситет: e = 5/3 ≈ 1.67.








